量子计算的重大突破正在撼动物理学和数学

1936年，艾伦·图灵（Alan Turing）揭示了“停机问题”，即无法通过算法确定计算机程序是否永远停止或循环的问题。现代计算机科学诞生了。它的成功给人的印象是很快所有实际问题都将转化为计算机的强大功能。

停机问题是逻辑数学中可计算性理论的一个问题。通俗地说，停机问题就是判断任意一个程序是否能在有限的时间之内结束运行的问题。该问题等价于如下的判定问题：是否存在一个程序P，对于任意输入的程序w，能够判断w会在有限时间内结束或者死循环。

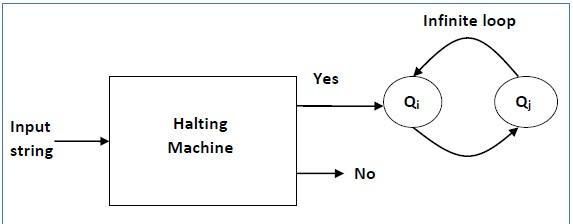
艾伦·图灵在1936年证明了不存在解决停机问题的通用算法。这个证明的关键在于对于计算机和程序的数学定义，这被称为图灵机。停机问题在图灵机上是不可判定问题，这是最早提出的决定性问题之一。

事情很快就变得很明显，尽管可以通过算法可以解决一些问题，但是实际的计算将使计算机需要持续很长的时间。仅仅通过算法找出解决问题的方法还不够。按效率对解决方案进行分类至关重要。复杂性理论根据解决问题的难度来对问题进行分类。问题的难度是根据计算持续时间来衡量的。

复杂性理论，也叫计算复杂性理论（Computational complexity theory），是理论计算机科学和数学中的一个分支，也是崭新的量子计算领域中的一个新的分支，指将可计算问题根据它们本身的复杂性分类，以及将这些类别联系起来。一个可计算问题被认为是一个原则上可以用计算机解决的问题，亦即这个问题可以用一系列机械的数学步骤，例如算法来解决。

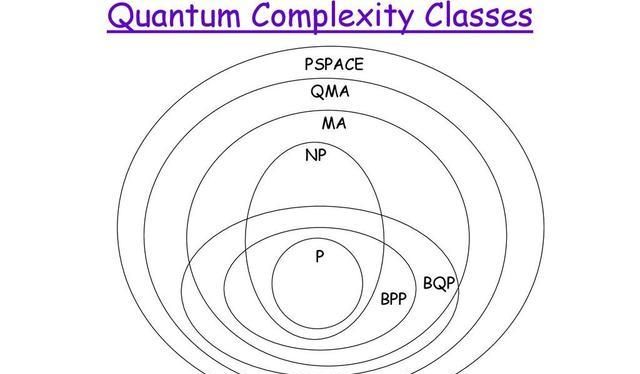
无论使用哪种算法，如果解决方案需要大量资源，则将其视为固有的难题。复杂性理论通过引入计算数学模型来研究这些问题并量化其计算复杂性，即解决这些问题所需的资源量，例如时间和存储，从而正式化了这种直觉。还使用其他复杂性度量，例如用于通信复杂性通信量，用于电路复杂性中门的数量、和用于并行计算的处理器数量等。

计算复杂度理论的作用之一是确定计算机可以做什么和不能做什么的实际限制，即P/NP问题。复杂度类P即为所有可以由一个确定型图灵机在多项式表达的时间内解决的问题；复杂度类NP由所有可以在多项式时间内验证它的解是否正确的决定问题组成，或者等效的说，那些可以在非确定型图灵机上在多项式时间内找出解的问题的集合。

P类包含已知算法可以快速解决的问题，在技术层面上是在多项式时间内。例如，将两个数相乘属于P，因为长乘法是解决该问题的有效算法。在P中不知道找到一个数的素因数的问题。该问题当然可以通过计算机解决，但没有已知的算法可以有效地解决。直到2004年，一个有效的算法表明该问题在P中时，一个相关的问题，即确定给定数是否为质数，处于类似的困境。

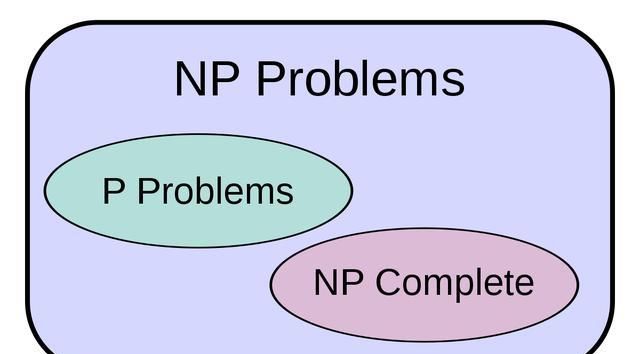
另一个复杂度类别是NP。想象一个迷宫，“有没有办法摆脱这个迷宫？”，这是一个是/否的问题。如果答案是肯定的，那么有一种简单的方法可以说服我们：只需向我们提供指示，我们将按照指示进行操作，然后找到出口。但是，如果答案是否定的，那么我们将不得不走遍整个迷宫，而永远都无法找到令人信服的出路。

这样的是/否问题，如果答案为是，我们可以有效地证明它属于NP。任何问题的解决方案都可以使我们相信答案，因此P包含在NP中。令人惊讶的是，P = NP是一个相当艰难的问题，没人知道。这个问题是一个在理论信息学中计算复杂度理论领域里至今未被解决的问题，也是七个千禧年大奖数学难题之一。

信任机器

到目前为止描述的类代表了普通计算机面临的问题。但是计算机正在发生根本性的变化，量子计算机正在开发与出现重大突破之中。如果出现了新型的计算机，并声称可以解决我们的问题之一，那么我们如何才能相信它是正确的呢？

以两个实体：询问者和证明者之间的交互情况为例。在警方或法庭的讯问中，被检举人试图证明自己是无罪的嫌疑人，询问者必须决定证明者是否具有足够的说服力。这里，存在一种认知上的不平衡：审讯者处于劣势。

在复杂性理论中，询问者是试图解决问题的人，其计算能力有限；证明者如一台新的计算机，它被认为具有巨大的计算能力。交互式证明系统是询问者可以使用的协议，以便至少以很高的概率确定是否应该相信证明者。以此类推，这些犯罪可能是警察或法庭无法解决的，但至少无辜者可以说服警察或法庭他们无罪，这是IP类。

如果可以询问多个证明人，并且不允许证明人协调其答案，如通常是警察或法庭询问多个嫌疑人的情况，那么我们进入了一个称为MIP的类别。这种询问通过交叉检验证明者的回答，为询问者提供了更大的能力，因此MIP包含IP。

量子通信是用量子位进行通信的一种新形式。纠缠是一种量子特征，即使分离，量子位也会被纠缠在一起，这使量子通信从根本上不同于普通通信。允许MIP证明者共享一个纠缠的量子位导致产生MIP*类。

　　影响深远

证明者之间的交流似乎只能帮助证明者协调谎言，而不能帮助审问者发现真理。因此，没有人期望允许更多的交流就会使计算问题变得更加可靠和得到解决。令人惊讶的是，前不久包括两名华人量子计算理论科学家在内的五位专家发表了一篇长达165页的论文，使我们现在知道：MIP* = RE（论文的标题）。这意味着量子通信的行为与正常通信完全不同。

在复杂性理论中，RE代表可以通过计算机解决的问题，是“复杂性类”计算问题的一个集合，如上面所述的P、NP、IP、MIP等只是这个集合中的一些子类。

在1970年代，著名法国数学家阿兰·康纳斯（Alain Connes）提出了所谓的“康纳斯嵌入问题”。这是关于冯·诺曼代数理论中的一个主要问题：询问无限矩阵是否可以由有限矩阵近似。现在，这份新论文证明了这是不可能的，对于纯数学家来说这是一个重要的发现。

同时，在1993年，鲍里斯·特斯雷尔森（Boris Tsirelson）指出了物理学中的一个问题，即特斯雷尔森问题。这是关于量子力学中一种情况的两种不同的数学形式问题，迄今为止一种数学形式非常成功地解释了亚原子世界的理论。作为同一现象的两种不同描述，人们预料这两种形式在数学上应该是等效的。

但是，这篇论文现在表明事实并非如此。可是究竟它们如何仍然可以产生相同的结果，并都描述相同的物理现实，这是个谜，但这就是为什么物理学家也突然对此感到兴趣的原因。

时间将说明对复杂性研究还有哪些其他未解决的科学问题。毫无疑问，MIP* = RE 是量子复杂性理论领域的一项突破性发现、巨大的飞跃。物理学家和数学家们现正在仔细研究这一论文，尽管可能并不完全了解或即时认知这些“复杂性类”计算问题的全部，但是事实证明，这一发现正在撼动物理学和数学，并对其产生惊人的影响。

　　参考：康纳斯嵌入问题：计算机科学中的里程碑式的数学证明